The channel coding and decoding technology can detect and correct errors introduced by the signal during transmission, and can ensure reliable transmission of data [1].
The check matrix of the LDPC code has sparse characteristics, so there is an efficient decoding algorithm, and its error correction capability is very strong. In 1981, Tanner proposed the concept of describing a codeword based on a graph model, and the check matrix of the LDPC code is mapped to the bidirectional bipartite graph of the Tanner graph. The LDPC code constructed by the Tanner graph can greatly reduce the decoding complexity by parallel decoding. Mack-ay and Neal used the randomly constructed Tanner graph to study the performance of LDPC codes. It was found that the LDPC codes using the sum product algorithm (SPA) have excellent decoding performance and even exceed the Turbo code in long codes [2]. The check matrix of the LDPC code is constructed using Mackay's improved scheme based on the bipartite graph. Based on the belief propagation (BP) algorithm, a simplified BP algorithm-logarithmic domain iterative APP LLR algorithm is presented, which greatly reduces the complexity. At present, the LDPC code is the most promising error correction technique for obtaining Shannon capacity in a wide range of channels [3]. Under the premise of ensuring the error correction performance of LDPC codes, reducing the complexity of the implementation of the codec is the focus of research. The research boom in the channel coding community.
1 LDPC code encodingThe LDPC code is a "good" code whose performance is very close to the Shannon limit. It is the only linear block code represented by the check matrix. The encoding of the LDPC code is mainly performed in two steps, first constructing a parity check matrix, and then an encoding algorithm based on a parity check matrix.
1.1 Construction of check matrixAccording to the expression n*j = m*k, the regular LDPC code (n, j, k), when the parameters n, j, k are determined, can obtain the number m of the check equation, and then the size of the check matrix H It can be set as m &TImes; n. The general steps for constructing the LDPC code check matrix are: to form an all-zero matrix of m rows and n columns, and then randomly replace j 0s in each column with 1, in each row. The k zeros are replaced by 1. However, in the process of randomly setting l, a ring of length 4 must be avoided [4].
If the minimum loop length is 4, it is very easy to cause the spread of error information in the iteration, which leads to the degradation of decoding performance [5].
In order to eliminate the length 4 ring in the check matrix, Mackay proposed an improved construction scheme based on the Tanner graph. The criterion adopted is: the construction must ensure that the overlap weight between any two columns does not exceed 1. This article uses Mackay's 1A construction method, an LDPC code (3,6) code constructed according to this method is shown in Figure 1. Show.

Mackay's 1A construction method is the most basic construction method, which requires that the fixed column weight be γ and the row weight be kept as Ï as uniform as possible.
The LDPC code obtained by the Mackay construction method has a good distance characteristic and has no short loop.
1.2 Parity algorithm based on parity check matrixThe direct encoding method of LDPC code is to use Gaussian elimination method to generate a lower triangular matrix, and then further elementary transformation to obtain the right unit matrix form H = [P|I], and obtain the generator matrix from G = [I|P], and then use the information. The symbol vector u and the generator matrix G are multiplied to obtain the complete codeword C, that is, C = M*G direct coding [5].
2 LDPC code decoding [4,6-7]The BP algorithm is based on the probability decoding algorithm proposed by Gallager. Each iteration of the BP algorithm consists of two steps: the processing of the variable node and the processing of the check node. The probability domain is the probability information transmitted between the nodes. Many multiplication operations are used, and the computational complexity is large. The logarithmic domain sum product algorithm realizes that the probability value is changed to the soft information value (LLR) through the log likelihood ratio. Passing, so that a large number of multiplication operations become additive operations, greatly simplifying the decoding complexity, and is conducive to hardware implementation. The following focuses on the logarithmic domain iterative APP LLR decoding algorithm.
2.1 Iterative APP LLR Decoding Algorithm Variable DefinitionFor the (N, K) LDPC code, the log likelihood ratio (LLR) when the variable U is defined to be 0 and 1 is:
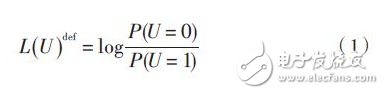
Let the codeword sent by the originator be u = [u1, u2,..., uN ], and the received codeword be y = [y1, y2,...,yN ], from which the check nodes and information passed in the iteration can be obtained. The soft information of the node is:
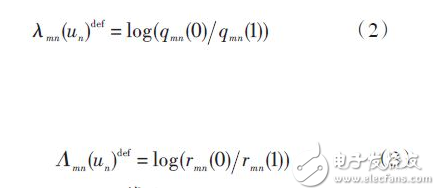
The iterative process of the iterative APP LLR decoding algorithm is as follows:
(1) Initialization: Let the soft information of each variable node n be:
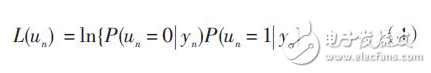
For H(m,n) = 1 in the matrix, the soft information of the corresponding variable node is initialized to the soft information of the channel output, ie λmn (un ) = L(un ), Λmn (un ) = 0.
(2) Check node update: According to each variable node n, the updated soft information is transmitted to all check nodes connected to the variable node, and the check node information is calculated:

Pneumatic Motor,Pneumatic Gear Motor,Small Pneumatic Motor,Pneumatic Vibration Motor
RUDONG HONGXIN MACHINERY CO.,LTD , https://www.rdhxmfr.com
