When a computer stores or moves data, a data bit error may occur. At this time, the Hamming code can be used to detect and correct the error. Simply put, the Hamming code is an error check code set, invented by RW Hamming of Bell Labs. Therefore, it was named Hamming code.
Hamming Code is a linear debugging code in the field of telecommunications, named after the inventor Richard Wesley Hamming. Hamming code inserts a verification code into the transmitted message stream to detect and correct single bit errors. Because Hamming codes are simple, they are widely used in memory (RAM). The SECDED (single error correction, double error detection) version additionally adds a detection bit to detect two or more simultaneous bit errors and correct single bit errors. Therefore, when the Hamming distance of the bit pattern of the transmitting end and the receiving end is less than or equal to 1 (only 1 bit error occurs), reliable communication can be realized. In contrast, a simple parity checker can detect only an odd number of errors in addition to correcting errors.
In mathematics, Hamming code is a binary linear code. For each integer, there is one code with one parity bit. The Hamming code of the parity check matrix is ​​independent of each other by listing the lengths of all the meters.
Hamming code definition and Hamming code inequality:Let: m = number of data bits, k = number of check digits, n = total number of coded bits = m + k, with Hamming inequality:
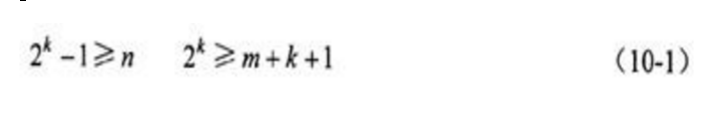
a) The total data length is N. If each bit of data is logged, it needs N bits to store.
b) Each check digit can represent: right or wrong; the check digit has a total of K bits, which can represent 2k states.
c) The total code length is N, so it contains a certain dislocation and a total pair of N+1 states.
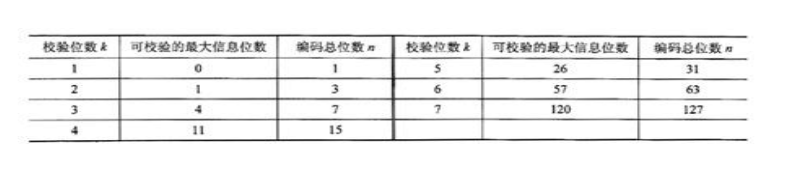
d) So 2k≧N+1 e) data table see below
Error correction of 2 or more digits cannot be achieved, and the Hamming code can only implement one bit of error correction.
Demonstrate the working process of Hamming code by taking a typical 4-bit data encoding as an example.
a) Data storage format:

According to the previous Hamming code inequality, when the data bit is 4 bits, the Hamming code check bit is at least 3 bits, arranged in the above manner.
It can be seen that the numbers in D8, D4, D2, and D1 are all integer powers of 2.
b) The insertion rule of Hamming check code:
Set: code bit code k, check code bit code p, data bit code n
A check code Pp will be at the kth position of the entire code
k=2^(p-1)=2 (p-1) power
Take a set of 9-digit codes with a data bit of 5 as an example, as follows:

c) Correspondence between check digits and data bits:
Note: ^ is a logical operator XOR.
P1=D8^D4^D1
P2=D8^D2^D1
P3=D4^D2^D1
Small explanation: The data bit has a total of 4 bits and each line is missing one bit, and the missing data bit is exactly DX. The check digit on the left side of the equation is PY, X=2y.
d) How the check digits participate in the calculation:
P1'=P1^D8^D4^D1
P2'=P2^D8^D2^D1
P3'=P3^D4^D2^D1
The binary number arranged from high to low: P3' P2' P1' indicates the error coded bit. There are 5 combinations from 000-011-101-110-111, which can indicate the original data bit D8D4D2D1. There are a total of five states in error.
e) Set a number: 1101, bring in the operation:
D8=1, D4=1, D2=0, D1=1,
P1 =1, P2=0, P3=0.
The result of Hamming code processing is 1010101
Assume: D8 error, P3' P2' P1' = 011 = decimal 3, which means that the third bit of the code is wrong, compared to the storage format table, it is a D8 error.
Assumption: D4 error, P3' P2' P1' = 101 = decimal 5, which means that the fifth bit of the code is wrong, compared to the storage format table, it is D4 error.
Flat Wire Power Inductors,Flat Copper Wire Inductors,Flat Coil High Current Inductors,Flat Wire High Power Inductors
Shenzhen Sichuangge Magneto-electric Co. , Ltd , https://www.scginductor.com
